Analysis and Control of a Suicide Dynamics Model

Suicide has become a major cause of human death during the last few decades. It is important to understand the dynamics of suicide and identify effective prevention strategies. In this work, bifurcation analysis and multi objective nonlinear model predictive control are performed on a suicide dynamics model. Bifurcation analysis is a powerful mathematical tool used to deal with the nonlinear dynamics of any process. Several factors must be considered, and multiple objectives must be met simultaneously. The MATLAB program MATCONT was used to perform the bifurcation analysis. The MNLMPC calculations were performed using the optimization language PYOMO in conjunction with the state-of-the-art global optimization solvers IPOPT and BARON. The bifurcation analysis revealed the existence of limit and branch points. The MNLMC converged on the Utopia solution (best possible). The limit and branch points (which cause multiple steady-state solutions from a singular point) are very beneficial because they enable the Multi objective nonlinear model predictive control calculations to converge to the Utopia point (the best possible solution) in the model. It is proved (with computational validation) that the branch points were caused because of the existence of two distinct separable functions in one of the equations in the dynamic model. A theorem was developed to demonstrate this fact for any dynamic model.

Suicide is a complex and multifaceted phenomenon that intertwines psychological, social, biological, cultural, and environmental factors in a deeply intricate web of causality. The dynamics of suicide encompass not only the individual’s internal struggles but also the external pressures and circumstances that shape their experience of the world. Understanding suicide dynamics requires a holistic view of the processes that lead a person from emotional distress to suicidal ideation, and in some cases, to the act itself. It is not a single event but a dynamic process unfolding over time, often marked by a series of warning signs, fluctuations in mood, cognitive distortions, and interactions with social contexts.

At the core of suicide dynamics lies the interplay between pain and hopelessness. Psychological theories, emphasize that suicide is often driven by unbearable psychological pain, or “psychache,” arising from frustrated needs and unresolved emotional conflicts. This pain does not exist in isolation but interacts with cognitive patterns that distort perception. When individuals lose the ability to envision a future where their suffering can be alleviated, hopelessness sets in as a powerful predictor of suicidal ideation. The sense that one’s situation is inescapable creates a cognitive narrowing that makes suicide appear as the only viable solution. This dynamic process involves a gradual erosion of coping mechanisms and a growing dominance of fatalistic thinking.

Neuroscience has contributed significantly to understanding the biological underpinnings of suicidal behavior. Alterations in neurotransmitter systems, particularly serotonin dysregulation, have been linked to impulsivity and aggression, traits often associated with suicidal actions. Neuroimaging studies show structural and functional changes in brain regions involved in emotion regulation, such as the prefrontal cortex, amygdala, and anterior cingulate cortex. These alterations influence how individuals process stress and emotional pain, making some more vulnerable to suicidal thoughts. Furthermore, genetic factors interact with environmental stressors to shape this vulnerability, suggesting that suicide results from an intricate dance between biology and lived experience. The biological component does not determine destiny but modulates sensitivity to the psychological and social factors that feed into suicidal crises.

Social dynamics play an equally vital role in shaping suicide risk. The influence of social isolation, loss of belonging, and the breakdown of community ties are central to many cases. Durkheim’s classical sociological theory identified suicide as a social fact, rooted in the degree of integration and regulation within a society. Too little integration, as seen in cases of egoistic suicide, leaves individuals detached from the social fabric, while excessive regulation or oppression can lead to fatalistic despair. In modern societies, rapid social change, technological isolation, and weakening family bonds have created new conditions under which feelings of alienation thrive. The sense of being disconnected from others can magnify psychological pain and reduce perceived sources of support, intensifying suicidal dynamics.

Cultural context also shapes the meanings attached to suicide. In some societies, suicide may be stigmatized and morally condemned, which can both prevent and conceal suicidal tendencies. In others, it may be viewed through a lens of honor, sacrifice, or protest, altering its social interpretation. Cultural narratives influence how individuals perceive suffering, resilience, and the acceptability of seeking help. The media plays a particularly important role in this cultural shaping. The phenomenon known as the “Werther effect” shows that detailed reporting or romanticization of suicide can trigger imitative behaviors, particularly among vulnerable individuals. Conversely, responsible media reporting that emphasizes prevention and recovery can have a protective “Papageno effect.” Thus, suicide dynamics extend beyond the individual psyche into the collective social imagination that frames how suicide is understood and discussed.

Psychological models have provided valuable frameworks for describing the sequence of events that lead to suicidal behavior. The interpersonal theory of suicide identifies three main components: perceived burdensomeness, thwarted belongingness, and acquired capability for suicide. These components interact dynamically over time. A person who feels like a burden and experiences social disconnection may develop a desire for death. However, transitioning from ideation to action requires the acquired capability, often gained through habituation to pain or exposure to traumatic experiences. This model underscores that suicidal behavior is not impulsive chaos but the outcome of a gradual and predictable psychological trajectory influenced by internal and external forces.

Another dynamic aspect of suicide lies in the fluctuation of suicidal ideation. It is not static but oscillates in intensity depending on emotional regulation, life stressors, and access to coping resources. Studies using real-time monitoring methods reveal that suicidal thoughts can vary significantly within hours or days. This temporal variability complicates prediction and intervention, as someone may appear stable shortly before an attempt. The dynamic nature of ideation emphasizes the importance of continuous support, real-time monitoring, and early intervention mechanisms. It also suggests that suicide prevention strategies must move beyond static risk assessments and toward adaptive, personalized approaches that account for the fluidity of human emotions.

The environmental and situational context often acts as the immediate trigger within this dynamic system. Financial stress, job loss, relationship breakdown, or chronic illness can precipitate crises in vulnerable individuals. The cumulative effect of multiple stressors overwhelms coping mechanisms and narrows perceived options. In such states, impulsivity may rise, and cognitive distortions deepen, leading to rash decisions. The availability of means also plays a critical role in suicide dynamics. Restricting access to lethal methods, such as firearms or toxic substances, has been shown to significantly reduce suicide rates. This demonstrates that even in moments of acute despair, the dynamics can be interrupted by environmental modifications that buy time for recovery and intervention.

Suicide prevention, therefore, must address the multifactorial and dynamic nature of suicidal behavior. Effective prevention operates at multiple levels: individual, social, and structural. At the individual level, therapeutic interventions like cognitive-behavioral therapy and dialectical behavior therapy aim to challenge distorted thoughts, improve emotion regulation, and build resilience. Social support networks act as buffers against isolation, offering empathy, validation, and belonging. On a structural level, policies that promote economic stability, access to healthcare, and destigmatization of mental illness are essential for reducing systemic risk factors. Prevention is not merely about reacting to crises but creating social environments that nurture connectedness, meaning, and hope.

The digital age has introduced new dimensions to suicide dynamics. Online communities can both help and harm. On one hand, virtual support groups and mental health resources provide access to help for those who might otherwise remain silent. On the other hand, exposure to harmful content, cyberbullying, and echo chambers that normalize suicidal thinking can exacerbate vulnerability. Algorithms that detect and flag distress signals on social media platforms have shown promise, but they raise ethical concerns regarding privacy and surveillance. Understanding suicide in the modern era requires integrating insights from psychology, sociology, and technology studies to design interventions that are both compassionate and effective.

Ultimately, suicide dynamics represent the convergence of personal suffering and societal failure. It is a phenomenon that cannot be understood solely through medical or psychological models but must also consider the moral and existential dimensions of human life. Many individuals who contemplate suicide are not seeking death but an end to their pain. Recognizing this distinction opens the door to empathy and prevention. Intervening in suicide dynamics means offering alternative narratives—ones that affirm life’s worth, validate suffering without judgment, and create spaces where despair can be spoken rather than silenced.

The dynamics of suicide are shaped by a complex interaction of biological predispositions, psychological vulnerabilities, social disconnection, cultural meanings, and situational pressures. These elements interact over time in non-linear and often unpredictable ways, producing patterns of risk that are unique to each individual. Suicide is not the inevitable outcome of distress but the product of dynamic systems that can be understood, interrupted, and transformed. By viewing suicide as a process rather than a moment, we gain the capacity to intervene earlier, build resilience, and cultivate societies where individuals feel seen, supported, and valued.

Maser, et al. [1] discussed whether temperament can identify affectively ill patients who engage in lethal or near-lethal suicidal behavior. Swann, et al. [2] showed that increased impulsivity is associated with the severity of suicide attempt history in patients with bipolar disorder. Baca-Garcia, et al. [3] discussed the connection between suicide attempts and impulsivity. Yip, et al. [4] researched the ecological fallacy and the gender ratio of suicide in China. Folly, et al. [5] developed a mathematical model for the nomothetic approach of suicide. Adinkrah, et al. [6] discussed the effect of criminal prosecution of suicide attempt survivors in Ghana. Osafo Joseph, et al. [7], encouraged understanding of suicidal behavior. Perry, et al. [8] discussed the best practices when working with suicidal behavior and self-harm in primary care with a qualitative exploration of young people’s perspectives. Quarshie, et al. [9] studied suicide attempts and deaths in older persons. Ossei, et al. [10] conducted research on the profile of suicide within the northern part of Ghana. Andoh-Arthur [11] studied the effect of economic difficulties and relational encounters before men’s suicide. Osman, et al. [12] modeled and performed optimal control studies of suicide dynamics in Ghana. In this work, bifurcation analysis and multiobjective nonlinear model predictive control is performed on the suicide dynamics model described in Osman, et al. [12]. The paper is organized as follows. First, the model equations are presented, followed by a discussion of the numerical techniques involving bifurcation analysis and multiobjective nonlinear model predictive control (MNLMPC). The results and discussion are then presented, followed by the conclusions.

Model equations [12]

The variables sbv, irv, ifv, sev, rv, represent susceptible individuals, individuals who attempted suicide that can be attributed to relationships, individuals who attempted suicide because of financial problems, and individuals who attempted suicide but recovered. The model equations are

$\begin{array}{l}\frac{d(sbv)}{dt}=\lambda -\left(1-u1\right)\rho (sbv)irv-\left(1-u1\right)\alpha (sbv)ifv-\mu (sbv)+\gamma (rv)\hfill \\ \frac{d\left(irv\right)}{dt}=\left(1-u1\right)\rho (sbv)irv-\left(\mu +\sigma \right)irv-u3\psi (irv)\hfill \\ \frac{d\left(ifv\right)}{dt}=\left(1-u1\right)\alpha (sbv)ifv-\left(\varphi +\mu \right)ifv-u2\tau (ifv)\hfill \\ \frac{d\left(sev\right)}{dt}=\sigma (irv)+\varphi (ifv)-\left(\mu +\delta \right)sev\hfill \\ \frac{d\left(rv\right)}{dt}=\tau (ifv)+\psi (irv)-\left(\gamma +\mu \right)rv\hfill \end{array}$ (1)

u1, u2, and u3 are the control variables and represent education, marriage counselling, and governmental financial intervention. The base values of the parameters are

$\begin{array}{l}\lambda =0.5;\alpha =0.3;\rho =0.2;\mu =0.1;\gamma =0.4;\\ \sigma =0.2;\varphi =0.3;\delta =0.15;\psi =0.35;\tau =0.25\end{array}$ (2)

These variables represent suicide recruitment rate, contact rate of financial-related suicide, contact rate of relationship-related suicide, natural death rate of all compartments, suicide recovery rate, relationship-related suicide death rate, financial-related Suicide death rate, Suicide induced death rate, Relationship recovery rate of suicide, and Financial recovery rate of suicide.

This model is based on data from the Ghana Police Service that shows the various incidents of suicide reported cases due to electrocution, hanging, drowning, and shooting.

Bifurcation analysis

Bifurcation analysis is performed using the MATLAB software MATCONT which locates branch points limit points and Hopf bifurcation points [13,14]. Consider a set of ordinary differential equations.

$\frac{dx}{dt}=f(x,\alpha )$ (3)

x ∈ Rⁿ with a bifurcation parameter be α. Since the gradient is orthogonal to the tangent vector,

The tangent $z=[z_1,z_2,z_3,z_4,\mathrm{....}{z}_{n+1}]$ must satisfy.

Az = 0 (4)

A is given by

$A=[\partial f/\partial x|\partial f/\partial \alpha ]$ (5)

Where ∂f/∂x is the Jacobian matrix. For both limit and branch points, the matrix must be singular. The n+1^th component of the tangent vector Z_n+1 = 0 for a limit point (LP) and for a branch point (BP) the matrix $B=\left[\begin{array}{l}A\\ z^T\end{array}\right]$ must be singular. At a Hopf bifurcation point,

$\det (2f_x(x,\alpha )@I_n)=0$ (6)

@ indicates the bialternate product and I_n is the n-square identity matrix. Hopf bifurcations cause limit cycles and should be eliminated because limit cycles make optimization and control tasks very difficult. More details can be found in Kuznetsov [15,16] and Govaerts [17].

Multiobjective Nonlinear Model Predictive Control (MNLMPC)

The procedure developed by Flores Tlacuahuaz, et al. [18] is used for performing the MNLMPC calculations Let the objective function variables ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ (j = 1, 2..n) for a problem involving a set of ODE

$\frac{dx}{dt}=F(x,u)$ (7)

Where tf is the final time value, and n the total number of objective variables and u the control parameter. First, the single objective optimal control problem independently and individually optimizing each of the variables. ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ is solved. Leading to the values $q_j^{*}$ . Then the multi objective optimal control (MOOC) optimization problem that will be solved is

$\begin{array}{l}\min ({\displaystyle \sum _{j=1}^n({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}-q_j^{*}){)}^2}\\ subjectto\frac{dx}{dt}=F(x,u);\end{array}$ (8)

This will provide the values of u at various times. The first obtained control value of u is implemented and the rest are discarded. This procedure is repeated until the implemented and the first obtained control values are the same or if the Utopia point where ( ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}=q_j^{*}$ for all j) is obtained.

Pyomo [19] is used for these calculations. Here, the differential equations are converted to a Nonlinear Program (NLP) using the orthogonal collocation method The NLP is solved using IPOPT [20] and confirmed as a global solution with BARON [21].

Sridhar [22] proved that the MNLMPC calculations to converge to the Utopia solution when the bifurcation analysis revealed the presence of limit and branch points. This was done by imposing the singularity condition on the co-state equation [23]. This makes the constrained problem an unconstrained optimization problem, and the only solution is the Utopia solution. More details can be found in Sridhar [22].

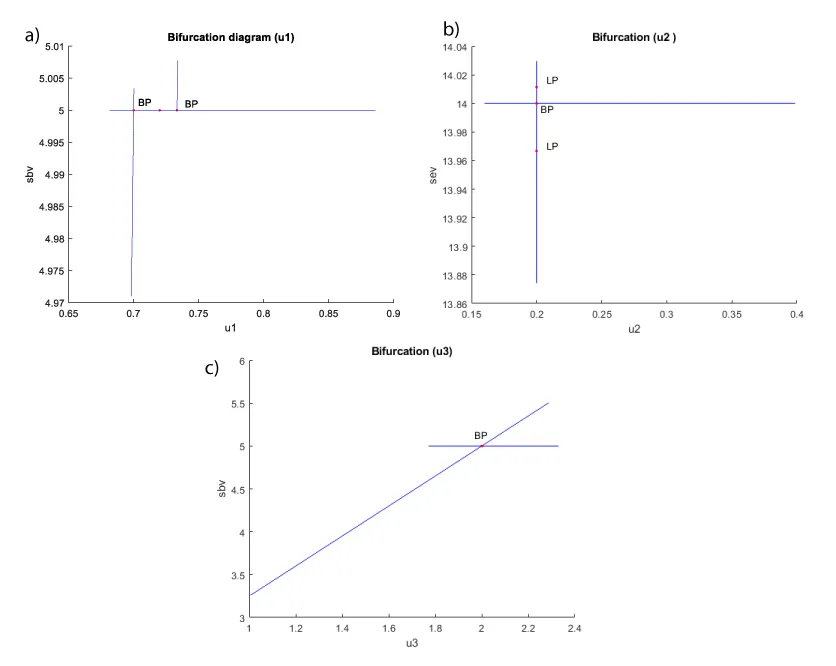
When u1 is the bifurcation parameter, two branch points were found at (sbv, irv, ifv, sev, rv, u1) values of (5, 0, 0, 0, 0,0.700000) and (5, 0, 0, 0, 0, 0.733333). (Figure 1a) When u2 is the bifurcation parameter, a branch point and 2 limit points were found at (sbv, irv, ifv, sev, rv, u2) values of (1.5, 17.5, 0, 14, 12.25, 0.2); (1.5,17.516144, -0.001291, 14.011365, 12.260655, 0.2); and (1.5, 17.452704, 0.003784, 13.966704, 12.218785, 0.2) (Figure 1b).

When u3 is the bifurcation parameter, a branch point was found at (sbv, irv, ifv, sev, rv, u1) values of ( 5, 0, 0, 0, 0, 2 )(Figure 1c).

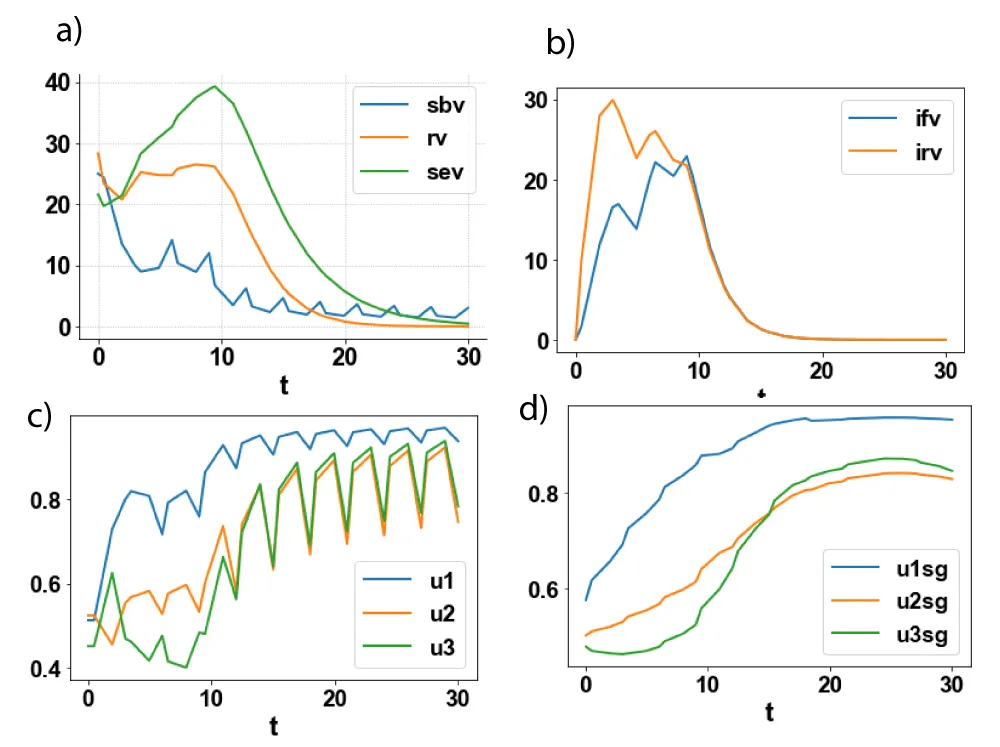
For the MNLMPC u1, u u3 are the control parameters, and ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}irv(t_i)},{\displaystyle \sum _{t_{i=0}}^{t_i=t_f}ifv(t_i)}$ were minimized individually, and led to values of 0 and 0. The overall optimal control problem will involve the minimization of ${({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}irv(t_i)-0})}^2+{({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}ifv(t_i)}-0)}^2$ was minimized subject to the equations governing the model. This led to a value of zero (the Utopia point). The MNLMPC values of the control variables, u1, u2, and u3 were 0.5123, 0.5241, and 0.45059. The MNLMPC profiles are shown in Figures 2a-2d. The control profiles of u1, u2, and u3 exhibited noise (Figure 2c) and this was remedied using the Savitzky-Golay filter to produce the smooth profiles u1sg, u2sg, and u3sg (Figure 2d).

Theorem

If one of the functions in a dynamic system is separable into two distinct functions, a branch point singularity will occur in the system.

Proof

Consider a system of equations,

$\frac{dx}{dt}=f(x,\alpha )$ (2)

x ∈ Rⁿ. Defining the matrix A as

$A=\left[\begin{array}{l}\frac{\partial f_1}{\partial x_1}\frac{\partial f_1}{\partial x_2}\frac{\partial f_1}{\partial x_3}\frac{\partial f_1}{\partial x_4}\mathrm{..........}\frac{\partial f_1}{\partial x_n}\frac{\partial f_1}{\partial \alpha }\\ \frac{\partial f_2}{\partial x_1}\frac{\partial f_2}{\partial x_2}\frac{\partial f_2}{\partial x_3}\frac{\partial f_2}{\partial x_4}\mathrm{..........}\frac{\partial f_2}{\partial x_n}\frac{\partial f_2}{\partial \alpha }\\ \mathrm{...........................................................}\\ \mathrm{...........................................................}\\ \frac{\partial f_n}{\partial x_1}\frac{\partial f_n}{\partial x_2}\frac{\partial f_n}{\partial x_3}\frac{\partial f_n}{\partial x_4}\mathrm{..........}\frac{\partial f_n}{\partial x_n}\frac{\partial f_n}{\partial \alpha }\end{array}\right]$ (3)

α is the bifurcation parameter. The matrix A can be written in a compact form as

$A=[\frac{\partial f_p}{\partial x_q}.|\frac{\partial f_p}{\partial \alpha }]$ (4)

The tangent at any point x; ( $z=[z_1,z_2,z_3,z_4,\mathrm{....}{z}_{n+1}]$ ) must satisfy

Az = 0 (5)

The matrix $\left\{\frac{\partial f_p}{\partial x_q}\right\}$ must be singular at both limit and branch points. The n + 1th component of the tangent vector Zn+1 = 0 at a limit point (LP) and for a branch point (BP) the matrix must be singular. Any tangent at a point y that is defined by $B=\left[\begin{array}{l}A\\ z^T\end{array}\right]$ ) must satisfy.

Az = 0 (6)

For a branch point, there must exist two tangents at the singularity. Let the two tangents be z and w. This implies that

$\begin{array}{l}Az=0\\ Aw=0\end{array}$ (7)

Consider a vector v that is orthogonal to one of the tangents (say z). v can be expressed as a linear combination of z and w ( $v=\alpha z+\beta w$ ). Since $Az=Aw=0$ ; $Av=0$ and since z and v are orthogonal, $z^{T}v=0$ . Hence $Bv=\left[\begin{array}{l}A\\ z^T\end{array}\right]v=0$ which implies that B is singular where $B=\left[\begin{array}{l}A\\ z^T\end{array}\right]$

Let any of the functions fi are separable into 2 functions φ₁, φ₂ as

fφ_i = φ₁ φ₂ (8)

At steady-state fφ_i(x, a) = 0 and this will imply that either φ₁ = 0 or φ₂ = 0 or both 1 and φ2 must be 0. This implies that two branches φ₁ = 0 and φ₂ = 0 will meet at a point where both 1 and are 0.

At this point, the matrix B will be singular as a row in this matrix would be

$[\frac{\partial f_i}{\partial x_k}|\frac{\partial f_i}{\partial \alpha }]$ (9)

However,

$\begin{array}{l}[\frac{\partial f_i}{\partial x_k}={\varphi }_1(=0)\frac{\partial {\varphi }_2}{\partial x_k}+{\varphi }_2(=0)\frac{\partial {\varphi }_1}{\partial x_k}=0(\forall k=1.,,n)\\ \frac{\partial f_i}{\partial \alpha }={\varphi }_1(=0)\frac{\partial {\varphi }_2}{\partial \alpha }+{\varphi }_2(=0)\frac{\partial {\varphi }_1}{\partial \alpha }]=0\end{array}$ (10)

This implies that every element in the row would be 0, and hence the matrix B would be singular. The singularity in B implies that there exists a branch point.

When u1 is the bifurcation parameter, two branch points were found at (sbv, irv, ifv, sev, rv, u1) values of (5, 0, 0, 0, 0,0.700000) and (5, 0, 0, 0, 0, 0.733333).

The first branch point occurs at (sbv, irv, ifv, sev, rv, u1) values of (5, 0, 0, 0, 0,0.700000). Here, the two distinct functions can be obtained from the second ODE in the model

$\frac{d\left(irv\right)}{dt}=\left(1-u1\right)\rho (sbv)irv-\left(\mu +\sigma \right)irv-u3\psi (irv)$ (11)

The two distinct equations are

$\begin{array}{l}irv=0\\ \left(1-u1\right)\rho (sbv)-\left(\mu +\sigma \right)-u3(\psi )\end{array}$ (12)

With irv = 0, u3 = 0, u1 = 0.7, sbv = 5, ρ = 0.2, σ = 0.2, µ = 0.1 both the distinct equations are satisfied validating the theorem.

The second branch point occurs at (sbv, irv, ifv, sev, rv, u1) values of (5, 0, 0, 0, 0,0.733333). Here, the two distinct functions can be obtained from the third ODE in the model

$\frac{d\left(ifv\right)}{dt}=\left(1-u1\right)\alpha (sbv)ifv-\left(\varphi +\mu \right)ifv-u2\tau (ifv)$ (13)

Here the two distinct equations are

$\begin{array}{l}ifv=0\\ \left(1-u1\right)\alpha (sbv)-\left(\varphi +\mu \right)-u2\tau =0\end{array}$ (14)

With ifv = 0, u2 = 0, u1 = 0.73333, sbv = 5, both distinct equations are satisfied validating the theorem.

When u2 is the bifurcation parameter, a branch point was found at (sbv, irv, ifv, sev, rv, u2) values of (1.5, 17.5, 0, 14, 12.25, 0.2).

Here, again the two distinct functions can be obtained from the third ODE in the model.

$\frac{d\left(ifv\right)}{dt}=\left(1-u1\right)\alpha (sbv)ifv-\left(\varphi +\mu \right)ifv-u2\tau (ifv)$ (13)

Here the two distinct equations are

$\begin{array}{l}ifv=0\\ \left(1-u1\right)\alpha (sbv)-\left(\varphi +\mu \right)-u2\tau =0\end{array}$ (14)

With ifv = 0, u2 = 0.2, u1=0, sbv = 1.5, , τ = 0.25, both distinct equations are satisfied validating the theorem.

When u3 is the bifurcation parameter, a branch point was found at (sbv, irv, ifv, sev, rv, u1) values of (5, 0, 0, 0, 0, 2). Here, again, the two distinct functions can be obtained from the second ODE in the model.

$\frac{d\left(irv\right)}{dt}=\left(1-u1\right)\rho (sbv)irv-\left(\mu +\sigma \right)irv-u3\psi (irv)$ (11)

The two distinct equations are

$\begin{array}{l}irv=0\\ \left(1-u1\right)\rho (sbv)-\left(\mu +\sigma \right)-u3(\psi )\end{array}$ (12)

With irv = 0, u3 = 2, u1 = 0, sbv = 5, ρ = 0.2, $\sigma =0.2,\mu =0.1,\psi =0.35,$ both the distinct equations are satisfied, validating the theorem.

The presence of the limit point and is beneficial because it allows the MNLMPC calculations to attain the Utopia solution, validating the analysis of Sridhar [22].

The described model is representative of many of the models subsequently by de Beurs, et al. [24], Olarte-Godoy [25], Schuerkamp [26], Gariepy, et al. [27], Pompili, et al. [28], and the results described in this paper can be applied to these models also.

Bifurcation analysis and multi objective nonlinear control (MNLMPC) studies were conducted on a suicide dynamics model. The bifurcation analysis revealed the existence of limit and branch points. The limit and branch points (which cause multiple steady-state solutions from a singular point) are very beneficial because they enable the Multi objective nonlinear model predictive control calculations to converge to the Utopia point (the best possible solution) in the model. It is proven (with computational validation) that the branch points were caused because of the existence of two distinct separable functions in one of the equations in the model. A theorem was developed to demonstrate this fact for any dynamic model. A combination of bifurcation analysis and Multi objective Nonlinear Model Predictive Control (MNLMPC) for a suicide dynamics model is the main contribution of this paper.

Data availability statement

All data used is presented in the paper

Conflict of interest

The author, Dr. Lakshmi N Sridhar, has no conflict of interest.

Dr. Sridhar thanks Dr. Carlos Ramirez and Dr. Suleiman for encouraging him to write single-author papers

1. Maser JD, Akiskal HS, Schettler P, Scheftner W, Mueller T, Endicott J, et al. Can temperament identify affectively ill patients who engage in lethal or near-lethal suicidal behavior? A 14-year prospective study. Suicide Life Threat Behav. 2002;32(1):10–32. Available from: https://doi.org/10.1521/suli.32.1.10.22183
2. Swann AC, Dougherty DM, Pazzaglia PJ, Pham M, Steinberg JL, Moeller FG. Increased impulsivity is associated with the severity of suicide attempt history in patients with bipolar disorder. Am J Psychiatry. 2005;162(9):1680–7. Available from: https://doi.org/10.1176/appi.ajp.162.9.1680
3. Baca-Garcia E, Diaz-Sastre C, Garcia-Resa E, Blasco H, Braquehais CD, Oquendo MA, et al. Suicide attempts and impulsivity. Eur Arch Psychiatry Clin Neurosci. 2005;255(2):152–6. Available from: https://doi.org/10.1007/s00406-004-0549-3
4. Yip PSF, Liu KY. The ecological fallacy and the gender ratio of suicide in China. Br J Psychiatry. 2006;189(5):465–6. Available from: https://doi.org/10.1192/bjp.bp.106.021816
5. Folly WSD. The threshold bias model: A mathematical model for the nomothetic approach of suicide. PLoS One. 2011;6(9):e24414. Available from: https://doi.org/10.1371/journal.pone.0024414
6. Adinkrah M. Criminal prosecution of suicide attempt survivors in Ghana. Int J Offender Ther Comp Criminol. 2013;57(12):1477–97. Available from: https://doi.org/10.1177/0306624x12456986
7. Osafo J, Akotia CS, Hjelmeland H, Knizek BL. From condemnation to understanding: Views on suicidal behavior in Ghana in transition. Death Stud. 2017;41(8):532–41. Available from: https://doi.org/10.1080/07481187.2017.1333357
8. Perry Y, Krysinska K, Byrne SJ, Boland A, Michail M, Lamblin M, et al. Best practice when working with suicidal behavior and self-harm in primary care: a qualitative exploration of young people’s perspectives. BMJ Open. 2020;10(10):e038855. Available from: https://doi.org/10.1136/bmjopen-2020-038855
9. Quarshie EN-B, Asante KO, Andoh-Arthur J, Asare-Doku W, Landindome NP. Suicide attempts and deaths in older persons in Ghana: A media surveillance approach. Curr Psychol. 2021;40(1):292–305. Available from: https://pure.ug.edu.gh/en/publications/suicide-attempts-and-deaths-in-older-persons-in-ghana-a-media-sur-3
10. Ossei PPS, Niako N, Ayibor WG, Asante E, Safo FK, Safowaa A. Profile of suicide within the northern part of Ghana: A decade under review. S Afr J Psychiatry. 2022;28:1620. Available from: https://doi.org/10.4102/sajpsychiatry.v28i0.1620
11. Andoh-Arthur J. Paradoxes of interdependence and dependence: A qualitative study of economic difficulties and relational encounters before men’s suicide in Ghana. Int J Qual Stud Health Well-being. 2023;18(1):2225935. Available from: https://doi.org/10.1080/17482631.2023.2225935
12. Osman S, Chukwu WC, Berhe HW, Gebrehiwot TA, Makinde OD, Otoo D, et al. Towards understanding suicide dynamics in Ghana: Modelling and optimal control application. Partial Differ Equ Appl Math. 2025;14:101187. Available from: https://doi.org/10.1016/j.padiff.2025.101187
13. Dhooge A, Govaerts W, Kuznetsov YA, et al. MATCONT: A Matlab package for numerical bifurcation analysis of ODEs. ACM Trans Math Softw. 2003;29(2):141–64. Available from: https://doi.org/10.1145/779359.779362
14. Dhooge A, Govaerts W, Kuznetsov YA, Mestrom W, Riet AM. CL_MATCONT: A continuation toolbox in Matlab. 2004.
15. Kuznetsov YA. Elements of applied bifurcation theory. New York: Springer; 1998. Available from: https://webspace.science.uu.nl/~kouzn101/pub.html
16. Kuznetsov YA. Five lectures on numerical bifurcation analysis. Utrecht University, NL; 2009.
17. Govaerts WJF. Numerical methods for bifurcations of dynamical equilibria. Philadelphia: SIAM; 2000.
18. Flores-Tlacuahuac A, Morales P, Riveral Toledo M. Multiobjective nonlinear model predictive control of a class of chemical reactors. Ind Eng Chem Res. 2012;51(17):5891–9. Available from: https://doi.org/10.1021/ie201742e
19. Hart WE, Laird CD, Watson JP, Woodruff DL, Hackebeil GA, Nicholson BL, et al. Pyomo – Optimization Modeling in Python. 2nd ed. Vol. 67. Springer; 2017. Available from: https://ideas.repec.org/b/spr/spopap/978-3-319-58821-6.html
20. Wächter A, Biegler LT. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program. 2006;106(1):25–57. Available from: https://doi.org/10.1007/s10107-004-0559-y
21. Tawarmalani M, Sahinidis NV. A polyhedral branch-and-cut approach to global optimization. Math Program. 2005;103(2):225–49. Available from: https://doi.org/10.1007/s10107-005-0581-8
22. Sridhar LN. Coupling bifurcation analysis and multiobjective nonlinear model predictive control. Austin Chem Eng. 2024;10(3):1107. Available from: https://austinpublishinggroup.com/chemical-engineering/fulltext/ace-v11-id1107.pdf
23. Upreti SR. Optimal control for chemical engineers. Boca Raton (FL): Taylor and Francis; 2013. Available from: https://doi.org/10.1201/b13045
24. de Beurs D, Bockting C, Kerkhof A, Scheepers F, O'Connor R, Penninx B, van de Leemput I, et al. A network perspective on suicidal behavior: understanding suicidality as a complex system. Suicide Life Threat Behav. 2021;51(1):115–26. Available from: https://doi.org/10.1111/sltb.12676
25. Olarte-Godoy J. Newtonian science, complexity science and suicide: Critically analysing the philosophical basis for suicide research: A discussion paper. J Adv Nurs. 2022;78(9):e101–10. Available from: https://doi.org/10.1111/jan.15346
26. Schuerkamp R, Liang L, Rice KL, Giabbanelli PJ. Simulation models for suicide prevention: a survey of the state-of-the-art. Computers (Basel). 2023;12(7):132. Available from: https://doi.org/10.3390/computers12070132
27. Gariepy G, Zahan R, Osgood ND, Yeoh B, Graham E, Orpana H. Dynamic simulation models of suicide and suicide-related behaviors: Systematic review. JMIR Public Health Surveill. 2024;10:e63195. Available from: https://doi.org/10.2196/63195
28. Pompili M, De Berardis D, Dell’Osso B, Forte A, Innamorati M, Rogante E, et al. Suicide and suicidal behaviors: Insight into clinical challenges and preventive measures. Expert Rev Neurother. 2025;25(9):1011–26. Available from: https://doi.org/10.1080/14737175.2025.2542764